1) Dois números somados totalizam 510. Sabe-se que um deles está para 8, assim como o outro está para 9. Quais são os dois números? Chamemos o primeiro número de a e o outro número de b. Do enunciado, tiramos que a está para 8, assim como b está para 9. Utilizando-nos da terceira propriedade das proporções temos:
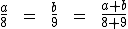
Sabemos que a e b somados resultam em 510, assim como a adição de 8 a 9 resulta em 17. Substituindo estes valores na proporção teremos:
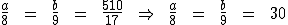
Portanto:
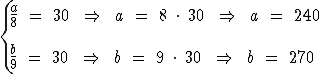
Chegamos então que os dois números são 240 e 270.
Sabemos que a e b somados resultam em 510, assim como a adição de 8 a 9 resulta em 17. Substituindo estes valores na proporção teremos:
Portanto:
Chegamos então que os dois números são 240 e 270.2) Um número a somado a um outro número b totaliza 216. a está para 12, assim como b está para 15. Qual o valor de a e de b? Recorrendo à terceira propriedade das proporções montamos a seguinte proporção:
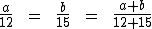
Sabemos que a soma de a com b é igual a 216, assim como também sabemos que 12 mais 15 totaliza 27. Substituindo tais valores teremos:
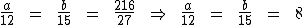
Portanto:
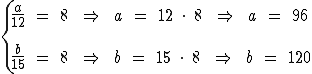
Os dois números são 96 e 120.
Sabemos que a soma de a com b é igual a 216, assim como também sabemos que 12 mais 15 totaliza 27. Substituindo tais valores teremos:
Portanto:
Os dois números são 96 e 120.3) Um número a subtraído de um outro número b resulta em 54. a está para 13, assim como b está para 7. Qual o valor de a e de b? Recorremos à terceira propriedade das proporções para montarmos a seguinte proporção:
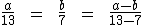
Sabemos que a diferença entre a e b é igual a 54, e sabemos também que 13 menos 7 dá 6. Substituindo tais valores teremos:
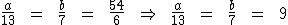
Portanto:
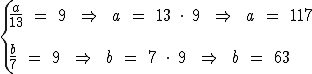
Os dois números são 117 e 63.
Sabemos que a diferença entre a e b é igual a 54, e sabemos também que 13 menos 7 dá 6. Substituindo tais valores teremos:
Portanto:
Os dois números são 117 e 63.4) A diferença entre dois números é igual a 52. O maior deles está para 23, assim como o menor está para 19. Quais são os números? Vamos chamar o número maior de a e o menor de b. Do enunciado, a está para 23, assim como b está para 19. Ao utilizarmos a terceira propriedade das proporções temos:
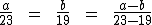
Sabemos que a menos b é igual a 52, assim como 23 menos 19 é igual a 4. Ao substituirmos estes valores na proporção teremos:
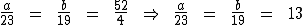
Portanto:
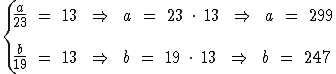
Chegamos então que os dois números são 299 e 247.
Sabemos que a menos b é igual a 52, assim como 23 menos 19 é igual a 4. Ao substituirmos estes valores na proporção teremos:
Portanto:
Chegamos então que os dois números são 299 e 247.5) A idade de Pedro está para a idade de Paulo, assim como 5 está para 6. Quantos anos tem Pedro e Paulo sabendo-se que as duas idades somadas totalizam 55 anos? Identifiquemos a idade de Pedro por a e a idade de Paulo por b. A partir do enunciado, temos que a está para b, assim como 5 está para 6. Utilizando-nos da segunda propriedade das proporções temos:
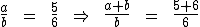
Sabemos que a soma a e b resulta em 55, assim como 5 mais 6 resulta em 11. Substituindo estes valores na proporção temos:
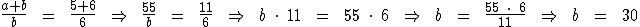
Para calcularmos o valor de a temos:
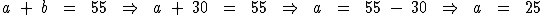
Portanto:
Pedro tem 25 anos e Paulo tem 30 anos.
Sabemos que a soma a e b resulta em 55, assim como 5 mais 6 resulta em 11. Substituindo estes valores na proporção temos:
Para calcularmos o valor de a temos:
Portanto:
Pedro tem 25 anos e Paulo tem 30 anos.6) O peso de uma sacola em kg está para o peso de uma outra sacola também em kg, assim como 32 está para 28. Quanto pesa cada uma das sacolas, sabendo-se que juntas elas pesam 15kg? Identifiquemos o peso da primeira sacola por a e o peso da segunda por b. Como expresso no enunciado, temos que a está para b, assim como 32 está para 28. Da segunda propriedade das proporções temos que:
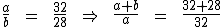
Temos que a e b somados resultam em 15, assim como 32 mais 28 resulta em 60. Substituindo-os na proporção temos:
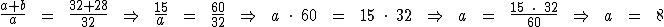
Calculemos o valor de b:
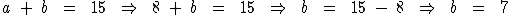
Portanto:
Uma das sacolas pesa 8kg ao passo que a outra pesa 7kg.
Temos que a e b somados resultam em 15, assim como 32 mais 28 resulta em 60. Substituindo-os na proporção temos:
Calculemos o valor de b:
Portanto:
Uma das sacolas pesa 8kg ao passo que a outra pesa 7kg.7) A soma de dois números é igual a 46. O primeiro está para o segundo, assim como 87 está para 51. Quais são os números? Identifiquemos o primeiro deles por a e o segundo por b. Como dito no enunciado, a está para b, assim como 87 está para 51. A segunda propriedade das proporções nos diz que:
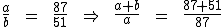
Temos que a mais b dá 46, assim como 87 mais 51 resulta em 138. Substituindo-os na proporção temos:
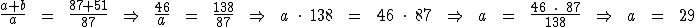
Calculemos o valor de b:
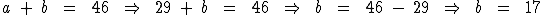
Portanto:
O segundo dos números é igual a 17 e o primeiro é igual a 29.
Temos que a mais b dá 46, assim como 87 mais 51 resulta em 138. Substituindo-os na proporção temos:
Calculemos o valor de b:
Portanto:
O segundo dos números é igual a 17 e o primeiro é igual a 29.8) Dois números a e b diferem entre si em 18 unidades. a está para b, assim como 825 está para 627. Qual o valor de a e de b? Da segunda propriedade das proporções temos:
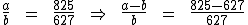
Sabemos que a diferença entre a e b resulta em 18, assim como 825 menos 627 resulta em 198. Substituindo tais valores na proporção temos:
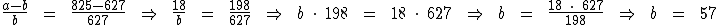
Para calcularmos o valor de a temos:
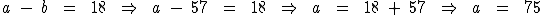
Portanto:
75 e 57 respectivamente se referem ao valor de a e de b.
Sabemos que a diferença entre a e b resulta em 18, assim como 825 menos 627 resulta em 198. Substituindo tais valores na proporção temos:
Para calcularmos o valor de a temos:
Portanto:
75 e 57 respectivamente se referem ao valor de a e de b.9) Quatro números, 72, 56, 90 e x, todos diferentes de zero, formam nesta ordem uma proporção. Qual o valor da quarta proporcional x? De acordo com a quarta proporcional temos:
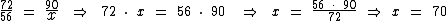
O valor da quarta proporcional x é 70.
O valor da quarta proporcional x é 70.10) Quatro números, x, 15, 15 e 9, todos diferentes de zero, formam nesta ordem uma proporção. Qual o valor da terceira proporcional x? De acordo com a terceira proporcional temos:
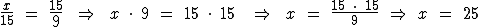
O valor da terceira proporcional x é 25.
O valor da terceira proporcional x é 25.
Nenhum comentário:
Postar um comentário